Recherche Google
OM 6.5 – User ManualScore Objects > Rhythm Trees > Rhythm Trees Structure
page précédentepage suivante

Rhythm Trees Structure

Traditionally, rhythm is broken up into several data : meter, measure(s) and duration(s). Rhythm trees must enclose these information in lists and sub list.

This elementary rhythm :

can be expressed as follows :

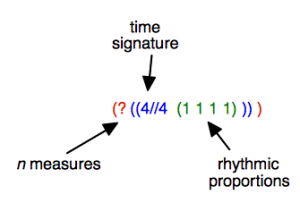
  • ( ? ( (4//4 (1 1 1 1) ) ) )
  • ( ? ( ( (4 4) (1 1 1 1) ) ) )

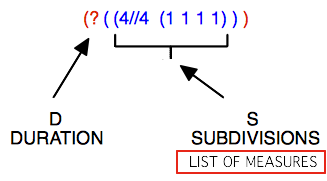
A tree structure can be reduced to a list : (D (S)).

Main Components : Duration and Subdivisions

  • D = a duration , or number of measures : ( ? ) or a number ( n ).

    When D = ?, OM calculates the duration.

    By default, this duration is equal to 1.

  • S = subdivisions (S) of this duration, that is a time signature and rhythmic proportions.

    1. Time signature = n // n   or ( n n ).

      It must be specified at each new measure, even if it remains unchanged.

    2. Rhythm = proportions : ( n n n n )

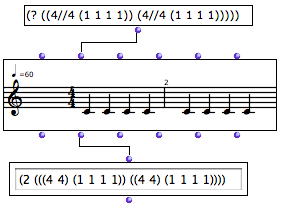Here, the (1 1 1 1) sub list represents four equal subdivisions of a 4/4 measure. OM calculated that the tree has two measures.
Here, the (1 1 1 1) sub list represents four equal subdivisions of a 4/4 measure. OM calculated that the tree has two measures.
Parenthesis Levels

A rhythm tree has at least three levels of parenthesis :

  1. number of measures

  2. list of measures

  3. time signature and proportions.

    Note that different rhythm trees with equal proportional structures produce the same rhythmic result :

    ( 1 1 1 1) = (2 2 2 2) = (124 124 124 124)

Durations

Manipulating Durations

By default, the duration of a measure is equal to 1. 1 represents the global measurement unit traditionally expressed by the time signature, such as : 4/4, 2/2  = ,  3/8 = etc.

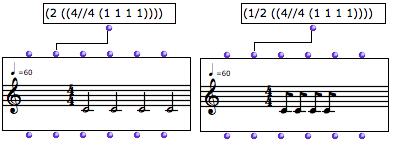
Changing this value multiplies or divides all the durations by a given coefficient.

Subdivisions : Measures and Groups

Measures

Trees define the way measures are split into proportional durations.

The following rhythm :

is written : ( ? ( (4//4 (1 2 1) ) ) ) .

Groups

Trees also define internal subdivisions, or groups[1] , within a measure.

The following rhythm :

is written : ( ? ( (4//4 (1 ( 2 (1 1 1) ) 1) ) ) ) .

Writing Groups

Note that groups must be written with a new subordinate level of parenthesis.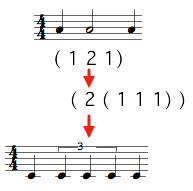

  1. Group

    An internal subdivision, that is, a list of proportions within a measure. A group can enclose a sub group. Basic examples are tuplets, groups of eighth, sixteenth notes. Groups of quarter, semibreves, whole notes or any other values are also admitted in rhythm trees.

    For instance :

    (? ((4//4 ( (2 ( 1 1)) (1 ( 1 (1 (1 1 1)))) (1 (1 1 1 1 1)) )))).

    This one measure tree has one group – two quarter notes – , one group with a sub group – one eighth note and a sixteenth notes triplet, and a last group – a quintuplet.

page précédentepage suivante
A propos...(c) Ircam - Centre PompidouRéalisé avec Scenari